Site Conditions
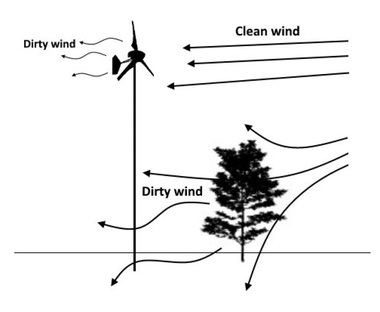
Answering the question of whether or not a wind turbine investment is right for you will first start with your location, or specifically where you can install your equipment and how suitable that location is for harnessing wind power, as well as the mean annual wind speed for the area. Any obstructions like buildings or tall trees standing between the energy source and the installation will have a negative effect on the performance of your system.
When it comes to harnessing clean wind (ie not turbulent) from a particular site, tower height matters. Like water, wind is a fluid and behaves accordingly. Any obstacles in the path of a wind stream will create turbulence, slow it down, and negatively affect performance from a wind turbine. Because of this, wind is typically the strongest and least turbulent above the tree canopy than it is below it. An ideal installation site would have an open area that allows a 30 meter radius around the turbine tower that's free of any obstacles that could affect the wind stream. The turbine itself should also be at least 10 meters above any nearby trees, if possible.
When it comes to harnessing clean wind (ie not turbulent) from a particular site, tower height matters. Like water, wind is a fluid and behaves accordingly. Any obstacles in the path of a wind stream will create turbulence, slow it down, and negatively affect performance from a wind turbine. Because of this, wind is typically the strongest and least turbulent above the tree canopy than it is below it. An ideal installation site would have an open area that allows a 30 meter radius around the turbine tower that's free of any obstacles that could affect the wind stream. The turbine itself should also be at least 10 meters above any nearby trees, if possible.
Energy Use
What you'll need for generation equipment will depend almost entirely on your daily energy requirements. This can be determined by referring to your monthly electricity bill to find your typical monthly energy usage expressed in kWh (kilowatt hours). Then divide that number by 30 to approximate how many kWh you use each day. (To be clear, kilowatt hours is a measure of energy, or the amount of work done over a period of time. Kilowatts, ie kilowatts per hour is a measure of power, or the rate that work is being done. So if we have a generator producing a constant 1 kW per hour for 1 hour, then it will have produced 1 kWh of work or energy. That same generator operating for 2 hours will produce 2 kWh of energy. kW per hour * hours in operation = kWh)
Notice the areas encircled on the bill below. The stated energy use for that month is 862 kWh. 862 / 30 days = 28.73 kWh used each day. Bare in mind that this was billed during the summer, when people generally use the least amount of energy in my region. It's always best to size your system for worst case scenario (ie winter demands). But for simplicity in the examples to follow, we'll stick to the usage stated on this bill.
Notice the areas encircled on the bill below. The stated energy use for that month is 862 kWh. 862 / 30 days = 28.73 kWh used each day. Bare in mind that this was billed during the summer, when people generally use the least amount of energy in my region. It's always best to size your system for worst case scenario (ie winter demands). But for simplicity in the examples to follow, we'll stick to the usage stated on this bill.
If you don't have a utility bill to refer to, then you can estimate how much energy you'll need by checking the power ratings of the devices, appliances or equipment that you want to power. If you want to power a water pump for a pond, for example, and it's rated for 110 volts and 5 amps, then you will need to find the total power in watts. Volts x Amps = watts, so 110V x 5A = 550W. Once you've determined the power rating, multiply that figure by how many hours that you expect it to operate during the day to figure out how much energy it will require. For instance 550W x 12 hours = 6600 watt hours, or 6600 / 1000 = 6.6 kWh per day. Do this with everything you intend to power, and add up the results for a total in kWh.
How To Size
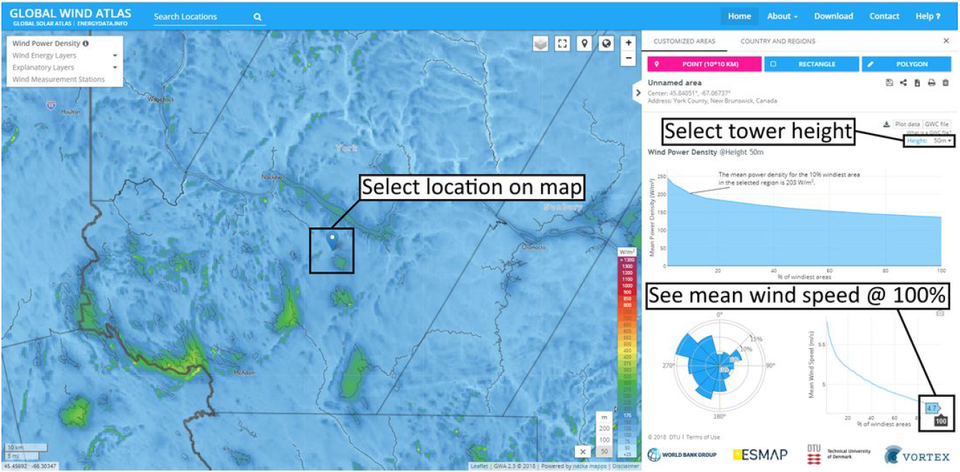
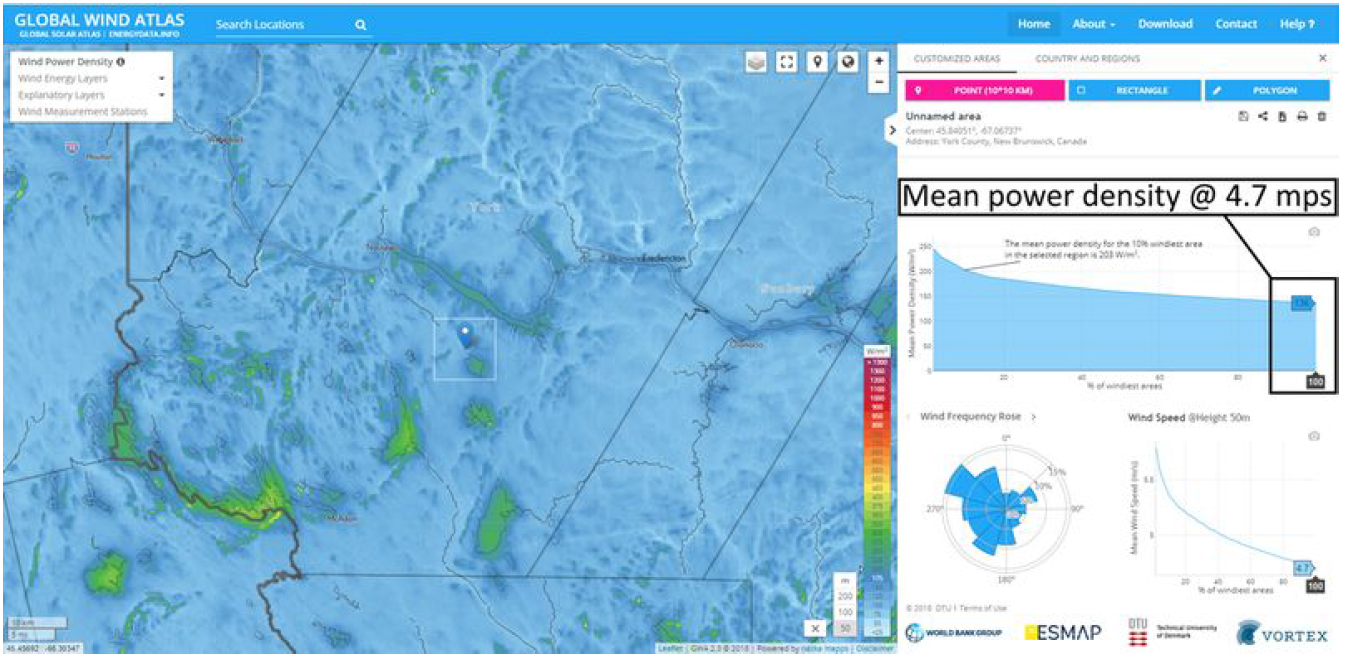
The first step in sizing a wind turbine is determining how much wind energy is available in your area. This can be done by visiting the globalwindatlas.info wind atlas mentioned previously. Select your location and tower height, and the page should then display a couple of graphs that show the mean wind speed and mean power density in watts per square meter based on the frequency distribution of the wind. See the images below.
The frequency distribution refers to how often the wind blows at different speeds over a period of time. The frequency distribution is also called the Weibull distribution, and is expressed as a Weibull shape parameter. In most areas of North America, the shape parameter will be ~2, or slightly above or below that number. This accounts for the variations in wind speed throughout the year at a given site. This means that the average annual output from a wind turbine at an average annual speed will usually be at least twice as much as the instantaneous power output from the turbine at that same instantaneous speed, given that the Wiebull distribution accounts for the rare output spikes that otherwise wouldn't be accounted for if a person were to simply multiply the instantaneous power output from a turbine at an instantaneous wind speed by 24 hours per day to estimate total kWh potential - the result of which would be much, much lower than the true potential of that site.
In the image above, the mean energy density for the area that I'd chosen is shown as ~136 watts per square meter of swept area at 4.7 mps wind speed. If, for example, we had a turbine with 1.83m blades creating a swept area of 10.5 sq.m, then the total amount of energy that’s available in a 10.5 sq.m wind stream at 4.7 mps is 136 x 10.5 = 1428 watts. But because of the Betz limit and the turbine coefficient, we’ll only be able to extract 30-40% of that energy. So the true mean energy density that can be extracted is 1428 x 0.3 = 428.4 watts. That’s a mean energy density of approximately 41 watts per sq. meter instead of 136. Keep in mind this is an average over time, and not instantaneous wind power.
To demonstrate how the Weibull distribution affects the mean annual output from a turbine at the mean annual wind speed, we can use the wind power equation to determine instantaneous power at the same instantaneous speed and compare the results:
P = 1/2ξpAV^3
= 1/2 [0.3 x 1.23 x 10.5 x (4.7 x 4.7 x 4.7)]
= 0.5 (0.3 x 1.23 x 10.5 x 103.82)
= 0.5 x 402.3
= 201.15 watts
So we can reasonably expect to see an instantaneous ~201 watts coming from the 10.5 sq.m turbine in a 4.7 sq.m wind stream. Now if we multiply that output by the Weibull parameter 2 (k), we can estimate the average output to be ~402 watts at the average wind speed of 4.7 mps. This is the difference between instantaneous power production at a given instantaneous wind speed at a given moment vs mean power production and mean wind speed over a period of time. When sizing your wind turbine, always base your calculations on the mean energy density and mean wind speed.
To demonstrate how the Weibull distribution affects the mean annual output from a turbine at the mean annual wind speed, we can use the wind power equation to determine instantaneous power at the same instantaneous speed and compare the results:
P = 1/2ξpAV^3
= 1/2 [0.3 x 1.23 x 10.5 x (4.7 x 4.7 x 4.7)]
= 0.5 (0.3 x 1.23 x 10.5 x 103.82)
= 0.5 x 402.3
= 201.15 watts
So we can reasonably expect to see an instantaneous ~201 watts coming from the 10.5 sq.m turbine in a 4.7 sq.m wind stream. Now if we multiply that output by the Weibull parameter 2 (k), we can estimate the average output to be ~402 watts at the average wind speed of 4.7 mps. This is the difference between instantaneous power production at a given instantaneous wind speed at a given moment vs mean power production and mean wind speed over a period of time. When sizing your wind turbine, always base your calculations on the mean energy density and mean wind speed.
To do that, you first need to find the true monthly energy production per 1 sq.m of swept area. Do this by multiplying the total mean energy density of the wind at the mean wind speed by a typical turbine coefficient of 30%. Then multiply that result by 24 hours to get the daily total, and then by 30 days for the monthly total:
136W x 30% = 40.8 watt per square meter true energy potential
40.8 x 24 hours = 979.2 watt hours, or 0.98 kWh per day
0.98 x 30 days = 29.4 kWh per month
Now we just need to divide the total monthly energy demand from the electric bill, by the monthly energy production available from 1 sq.m of swept area to determine the size of turbine needed to meet the demand:
862 kWh demand / 29.4 kWh per month per sq.m = 29.3 sq.m
So to meet the 862 kWh per month demand, a turbine with a 29.3 sq.m swept area is needed. In terms of blade length, that would be the square root of the result of 29.3 sq.m / Pi, which would be 3 meters, or 9 feet and 10 inches. This is quite a large wind turbine, maybe too large for a DIY’er to tackle on their own. However, two smaller turbines with half of the required swept area would suffice, as well. This would reduce the size and weight of the components used, and make them more easy for one or two people to construct, handle, and service in the future. It would also offer some redundancy in case one turbine breaks down.
136W x 30% = 40.8 watt per square meter true energy potential
40.8 x 24 hours = 979.2 watt hours, or 0.98 kWh per day
0.98 x 30 days = 29.4 kWh per month
Now we just need to divide the total monthly energy demand from the electric bill, by the monthly energy production available from 1 sq.m of swept area to determine the size of turbine needed to meet the demand:
862 kWh demand / 29.4 kWh per month per sq.m = 29.3 sq.m
So to meet the 862 kWh per month demand, a turbine with a 29.3 sq.m swept area is needed. In terms of blade length, that would be the square root of the result of 29.3 sq.m / Pi, which would be 3 meters, or 9 feet and 10 inches. This is quite a large wind turbine, maybe too large for a DIY’er to tackle on their own. However, two smaller turbines with half of the required swept area would suffice, as well. This would reduce the size and weight of the components used, and make them more easy for one or two people to construct, handle, and service in the future. It would also offer some redundancy in case one turbine breaks down.